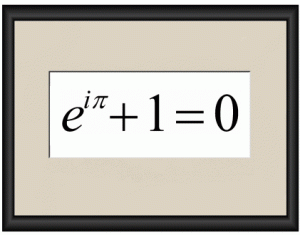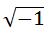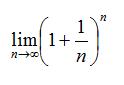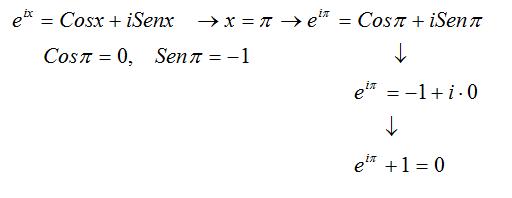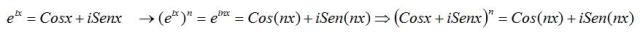Seguro que muchos de vosotros ya os habéis fijado que algunos profes de mates llevamos escrita una fórmula en nuestras batas:
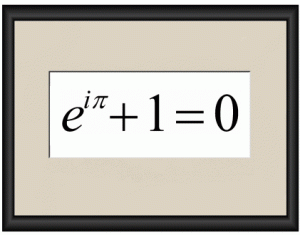
Pero, ¿Por qué esa fórmula y no otra? Podíamos haber elegido el Teorema de Pitágoras, que es probablemente la fórmula matemática más famosa, o la Relación Fundamental de la Trigonometría (y así de paso os serviría de “ayuda” en los exámenes…) En cambio hemos elegido la FÓRMULA DE EULER, la que sin lugar a dudas es la FÓRMULA MÁS BONITA DEL MUNDO, sí, habéis leído bien, hemos dicho BONITA y no, no nos hemos vuelto locos.
Al igual que admiramos la belleza de “Las Meninas” de Velázquez , “El Beso” de Gustav Klimt o “La Piedad” de Miguel Ángel,también hay fórmulas que tienen esa capacidad de transmitir armonía, elegancia y belleza a aquel que sepa apreciarlo.
Y es que, en la fórmula de Euler aparecen, de la forma más simple y sencilla, los cinco números más importantes de la Historia de las matemáticas: 0, 1, π, i y e.
El número 0
Aunque hoy en día vemos el 0 como un número fundamental en el engranaje de las matemáticas, no siempre ha estado presente. En la antigüedad (allá por el año 10000 a.C.) las antiguas civilizaciones el único concepto de número que tenían era “mucho” o “poco”, hasta que sintieron la necesidad de contar aquello que poseían y así comenzaron a contar: 1, 2, 3… empleando para ello los dedos de las manos (por eso nuestro sistema de numeración es decimal).
Así se construyó, de forma aditiva, la sucesión de los números naturales. Pero en aquella época, nadie sentía la necesidad de contar “la nada” por eso ni la civilización egipcia, ni la griega, que destacaron por sus amplios conocimientos de aritmética, geometría y astronomía, nunca introdujeron el símbolo del cero.
Fueron los calculistas indios los que dieron por primera vez una definición del Cero: El resultado de sustraer cualquier número de sí mismo y le denominaron “shunya” que significa vacío.
Pero, ¿Por qué es tan importante el 0? El 0 es el único número que no es ni positivo ni negativo, además tiene unas reglas propias ya que es el único número que si lo colocas a la izquierda de otro, no modifica su valor.
¿y qué ocurre con las operaciones aritméticas? Si a un número cualquiera le sumas o restas 0 se queda igual, si le multiplicas por 0 se anula, ¿y si lo divides entre 0? Entonces es mucho más curioso aún ya que se convierte ¡en infinito! ¿y si a 0 lo divides entre 0? Entonces llegamos a lo que en matemáticas se denomina INDETERMINACIÓN.
El número 1
El número es la esencia de todas las cosas decía Pitágoras y la esencia de nuestro sistema numérico es el 1. Él es el primer número de los Naturales y la base sobre la que se construyen, ya que cada número natural proviene de sumar 1 unidad al anterior.
El 1 es el elemento neutro del producto y el único número natural que no es ni primo ni compuesto, ya que, en el conjunto de los naturales, un número es primo si tiene dos divisores, el 1 y él mismo, y es compuesto si tiene más de dos divisores y como el 1 sólo es divisible por él mismo, no se ajusta a ninguna de las dos definiciones, siendo así un número especial, ni primo, ni compuesto.
El número π
Pero si hay un número que ha fascinado a científicos de todas las épocas, ese es π.
La definición nos dice que π es el número que se obtiene al dividir la longitud de una circunferencia por su diámetro y lo encontramos por primera vez en el Papiro Rhind (1650 a.C.) y en el Papiro de Moscú (1850 a.C.) que aproximaban su valor a 3.16049.
En la actualidad, gracias a los ordenadores, conocemos más de 10 billones de cifras de π. Pero lo más curioso de este número son sus propiedades, en primer lugar es un número irracional, es decir, posee infinitas cifras decimales no periódicas, por lo que no puede ser expresado en forma de fracción. También es un número trascendente ya que no es solución de ninguna ecuación polinómica con coeficientes racionales. Además aparece en la solución de numerosas series y multiplicaciones infinitas y es fundamental en el estudio de los números complejos.
El número i
René Descartes decidió denominar i a la raíz cuadrada de -1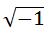
¡PERO ESO ES IMPOSIBLE! No existe la raíz cuadrada de los números negativos -diréis algunos- por eso le llamó número imaginario. A partir de este número se ha creado el conjunto de los números complejos, con sus reglas de operación y sus propiedades definidas al igual que el resto de conjuntos numéricos. Este número, que puede parecer un “invento” del hombre, tiene gran importancia en Física, en electromagnetismo, ondas radioactivas, trayectorias espaciales, aerodinámica…
El número e
El número e debe su nombre a uno de los matemáticos más importantes de la historia, Leonard Euler, y es el resultado del siguiente límite: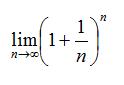 
A medida que crece el valor de n, la sucesión va aumentando su valor, sin embargo, cuánto mayor es el valor de n más despacio crece. El límite de dicha sucesión es e = 2,718281828459….
Pero, ¿Qué tiene de interesante esta sucesión para querer hallar con tanta precisión su límite? Pues es ni más ni menos que la ley de crecimiento, es decir, la ley por la que se rigen el crecimiento de las bacterias, el crecimiento de un capital con un interés compuesto, el crecimiento de los habitantes de una población… cualquier magnitud susceptible de multiplicarse a un ritmo constante cada cierto tiempo. Además éste número e, al igual que π es irracional y trascendente.
Por eso nos fascina tanto una fórmula que de forma simple y sencilla es capaz de unir a estos 5 magníficos números, pero por lo visto, la FÓRMULA DE EULER no nos gusta sólo a los matemáticos, también hay algún “graffitero” que ha apreciado su elegancia y así lo ha plasmado en una pared de San Lorenzo de El Escorial.
A lo mejor lo que no sabe el grafittero de San Lorenzo es porqué en esa fórmula hay un más en vez de un menos, y es que esta expresión es un caso particular de la fórmula general de Euler:
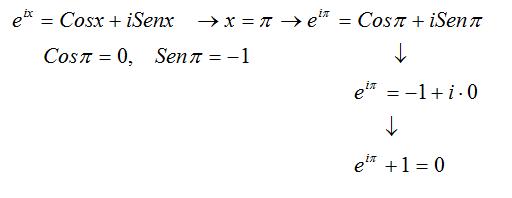Y seguro que tampoco sabe que fue en el año 1707 cuando el matemático francés Abraham De Moivre demostró a partir de esta igualdad la conocida como Fórmula de Moivre:
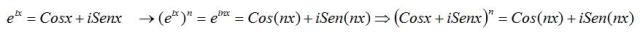
pero no vamos a profundizar más en este post, ya que se ve que el tema empieza a complicarse.
Ahora ya sabéis que la fórmula más bella de la historia de las Matemáticas es la “Fórmula de la bata”
Blog del Departamento de Matemáticas 